Clearhat

I tried for years to get a clear intuitive image for the inside of a sphere, as clear as I already have for the outside of a sphere. It's really hard! I've even been inside a large spherical room (there's a church in Boston with one), and of course, as we all do, I can easily imagine being inside of a cubical room. But it's hard to imagine being inside a sphere, for some reason.

When I imagine a normal sphere (from the outside), it appears suddenly in my imagination, and I'm able to zoom in or out, color it any color, make it pear-shaped, basically manipulate it in any way while comparing it to other imagined items, and I assume most people can do this also. But try and imagine the inside of a sphere. For me, elements of the idea come in to play, but they're hard to contain, kind of like infinity; it really takes some effort to imagine it. I think it's because, to do it properly, we have to place our awareness *inside* the sphere, and look outward. This is not a normal view. Usually we like to see things from the outside.

You know how a fisheye lens distorts things, right? Well it's kind of like that, the idea is not intuitive until you spend some time on it, sorting out what's happening, and then you're able to piece together the smooshed elements into a coherent picture. (Almost as an aside, here's a web page by a guy describing what it looks like from inside a spherical mirror. It's .... definitely weird, I'll say that. Not simple and intuitive at all. There's a lot going on, depending on where you are within the sphere. The moment where you suddenly flip upside down is particularly startling. In short, the inside of a sphere is NOT as perceptually simple as the outside of a sphere. It's like a completely different experience intuitively, even though they're two sides to the same coin, er, the same soap bubble.)

The reason I kept working at this intuition for years is because I was trying to develop various thought experiments in mathematics and physics, and would occasionally run into this challenge. Over time I became familiar with how hard it is to intuit the inside of a sphere, and I assume that it's hard for most people. I'd like to have conversations with someone for whom it is easy.

The other day, I was reading an article on Wikipedia about the different kinds of geometries (elliptic, Euclidean, and hyperbolic) and I came across a familiar image: a sphere, a plane, and a saddle. I've seen it many times over the years, but this time, the third frame jumped out at me. I immediately saw that the "saddle" illustration is completely out of place. It's too complicated! Just like Euclid's famous fifth postulate -- the modification of which is actually the origin of these three geometries -- it looked anomalous. It should be more simple. For the first time, I began to see in my mind's eye, quickly and efficiently, the inside of a sphere. It's hard to draw, but I can see immediately it's a simpler object than that saddle. To capture the idea, I modified the drawing, and you can see what I mean. The frame on the bottom right is my version of the well-known saddle idea which is shown immediately above it, in the top right with an X through it:

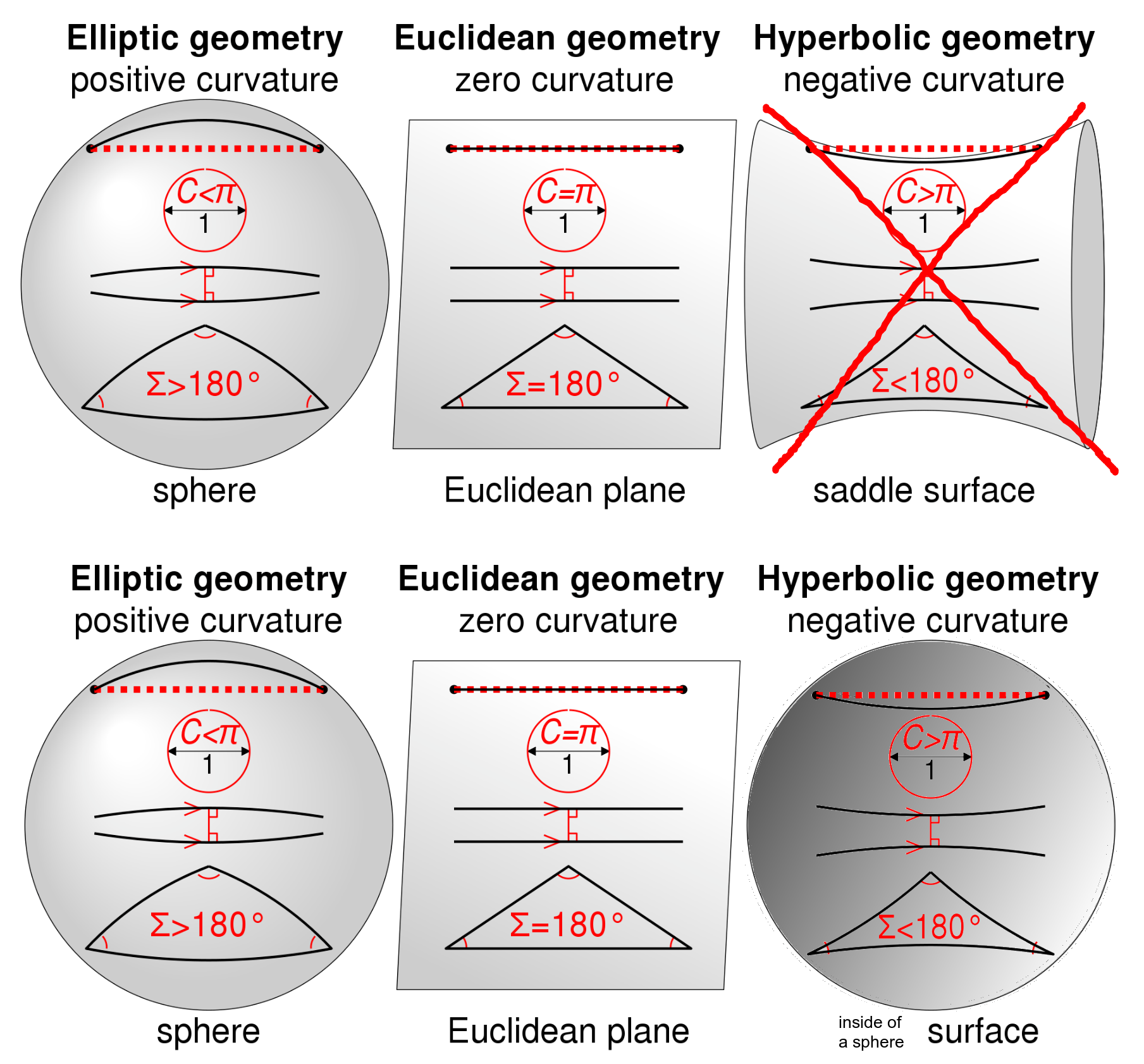
It's a crude drawing, but you get the idea. Now of course, nearly every mathematician out there will quickly tell me that the inside of a sphere is identical with the outside of a sphere as far as Gaussian curvature is concerned. For example, here is someone else who had the same idea as me a while back, and it was quickly shot down:

StackExchange: Is the inside of a sphere a hyperbolical surface? (tl;dr: the answer is no.)

Okay, so I know that I'm wrong, and I'm certainly not smart enough to joust with Gauss, so why go further and write this little article? Well, here's where the story gets interesting.

Long time readers of mine will note that I approach math a little differently from the norm, coming at it with suspicion of anything that incorporates the "excluded middle," (which includes set theory, and is therefore almost everything. Note that I don't reject such ideas so much as I just think they can be better organized).

Although there are other finitists and ultra-finitists like me out there, as far as I can tell, none of the other finitists also have an obsession with ternary logic like I do. Ternary logic provides another layer of insight into why finitist math -- also known as "computable math" because it is what digital computers do -- is the correct approach to infinity. (In other words, we're "finitists" because there is no "infinity," as set theory has postulated for the past century, relying on a version of infinity that is incoherent to us finitists.)

To sum my unique angle from a ternary logic perspective: Everyone is used to perceiving the world using an inherited perceptual system which relies on binary logic. This is a condition tracing back to at least the time of Aristotle, who was one of the first writers to talk about binary logic and its necessary reliance on the "excluded middle." It's like we have a layer of interpretation happening in our minds which flattens the 3D world, in order to more easily make logical sense of it. Although this effect is quite obvious when going to see a movie, and there we perceive everything within a 2D screen for a couple hours -- and our brain just does it natively, this flattened sense of perception was even more pervasive during the "dark ages" before artistic perspective was invented.

Paintings lacked any depth perception, and they look flat to our better depth-trained eyes. Although we have learned to see and create artwork with perspective, that ancient underlying 2D perceptual framework is still pervasive, to this day, in everything we see, think, feel, and do from early childhood upward.

Note that binary logic is also embedded in language, not just the visual field, and nobody has "invented perspective" for language yet. Hence we take all this for granted, and except for a few rare academic specialists, nobody even knows this is happening, because nobody has studied ternary logic deeply enough to see binary logic for what it is from the outside. It is truly everywhere. It is something we are taught without realizing it.

After having studied this phenomenon for a couple decades, it is clear to me that we are only a little more advanced than the middle ages, perceptually. I've noticed that even physicists who work closely with Einstein's ideas -- devloped by Riemann -- tend to remain in a fairly "Euclidian" way of thinking about Riemannian concepts, if that makes any sense.

Because binary logic is embedded in our language and culture so deeply, we don't know how to think outside that box -- or even that we can -- and thus it takes years to learn how to see things outside of this frame (a long process which I've written about previously). However, once you step outside that box, a lot of basic assumptions about the way math operates need to be re-evaluated.

It's kind of like the difference between "normal" vector-based geometry and Algebraic Geometry. In other words, Clifford's algebraic geometry is far more intuitively organized, and learning it is easier yet it powerfully provides all kinds of implicit insights into the laws of physics which are missing in, say, legacy vector-based geometry with its dependence on Euclid's excluded middles.

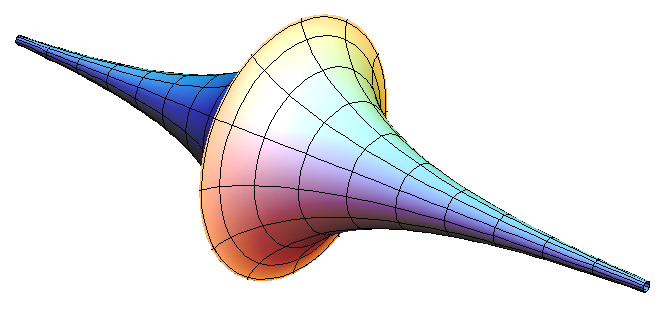One thing I know for sure, the pseudosphere is even more complicated and non-intuitive than that saddle. I can't think of anything in Nature that even has that shape naturally. To me it looks like an obvious hacked attempt to draw the inside of a sphere without drawing the inside of a sphere, but I get that not everyone will see that.

Update, March 1 2021: Okay so I'm still contemplating this idea, and researching it. I'm well aware that my idea, as expressed above, is mathematically absurd, but I also know the underlying intuition that I'm working with is solid, and I have good reason (more than just a hunch) to believe this insight is invisible, hidden from others whose perceptions are embedded in 2D, which explains why people have missed something so obvious. Here's the latest. Take a look at this illustration from Wikipedia on the three different geometries:

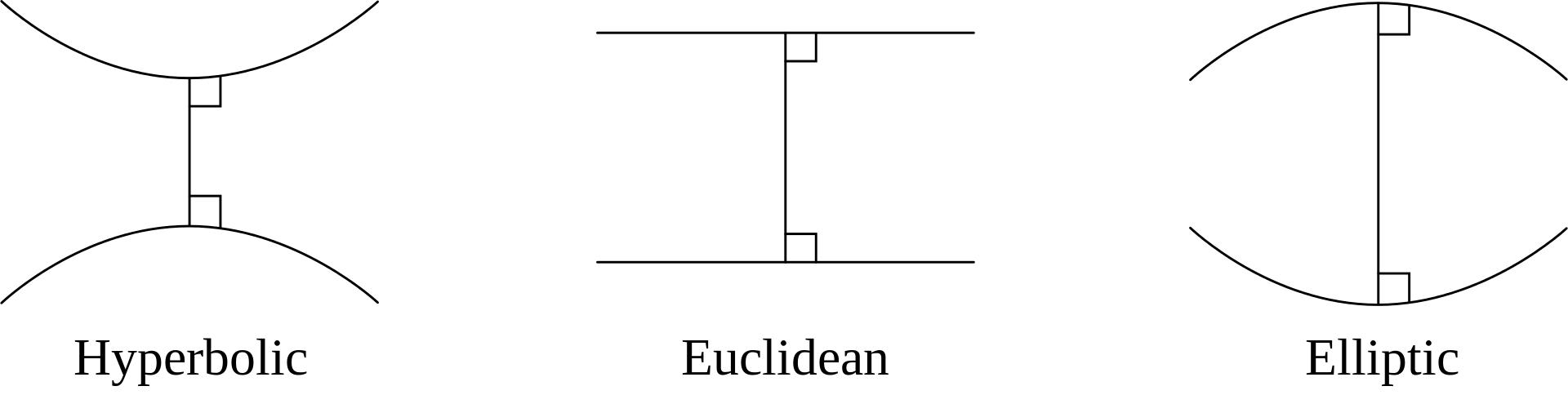
This portrayal is more simple, abstract, and sensible than the first illustration. Here, "hyperbolic" is only superficially saddle-shaped. The actual point being made with the illustration is a little deeper than what is visible with the saddle.* But, I have a hunch even you, dear reader, can admit a circle is much more like "the inside of a sphere" than the very anti-spherical-looking four-cornered saddle being illustrated here, if you'll permit the analogy. And if you accept that, you're half way to seeing what I'm seeing.

Note, it's the simplicity of the circle that I'm emphasizing. The saddle is not as simple as another concept that fits the parameters which the saddle was invented to describe, so we should at least consider the other thing.

I now think there is a subtle conflation between the three forms of Gaussian curvature and the three different geometries, a correlation which is somehow missing something, but I haven't been able to pinpoint how yet. That will take more research, possibly a lot more. Gauss was a genius and is likely to have some insight on this, but I'm guessing in an obscure way that might take some digging.

While pursuing these thoughts, I took a little plastic sphere, which is able to be opened up, and drew a triangle inside of it. If you look straight down into the sphere, the triangle looks like an ordinary triangle, as if it adds up to 180 degrees like in Euclidean space. But if you look at it from the side, you can clearly see that the sides of the triangle bow inward, just like the triangle in the original hyperbolic sphere illustration I drew above. Take a look:

If that's not enough to convince you I'm onto something, take this one step further. You can easily imagine what happens if you draw the same triangle on the outside of the sphere, because exactly the same thing happens. In other words, the lines bow inward no matter whether you draw them on the inside of the sphere or on the outside. Which means that the top left image in the first illustration above (labeled "Elliptic geometry"), with triangle lines bowing outward, is not accurately representing a triangle drawn on an elliptical (spherical) surface. Those lines will bow inward, just like they do on the inside of the sphere unless you purposely make them bow outward to match the illustration above. All of this is getting verrrrry curious, at the very least, and hence this problem is not leaving my imagination alone.

Update, later still: Okay, so I finally found an article that goes into the correct detail to get to the bottom of this. Skimming through it, I'm even more convinced that the existing intuitions for hyperbolic space are -- like many other intuitions embedded within binary logic -- flawed (or at the very least, "inaccurate maps" of the "territory"). Consider the following illustration, called a "two-sheet hyperbola." I can't believe the two-sheet hyperbola (mentioned in numerous places as a canonical way to illustrate hyperbolic space), which is so obviously a sphere cut in half and turned inside out, is illustrated so boldly and people still can't see what's going on here! But then again, yes I can. Check out this illustration, you'll see it immediately now that you know what to look for:

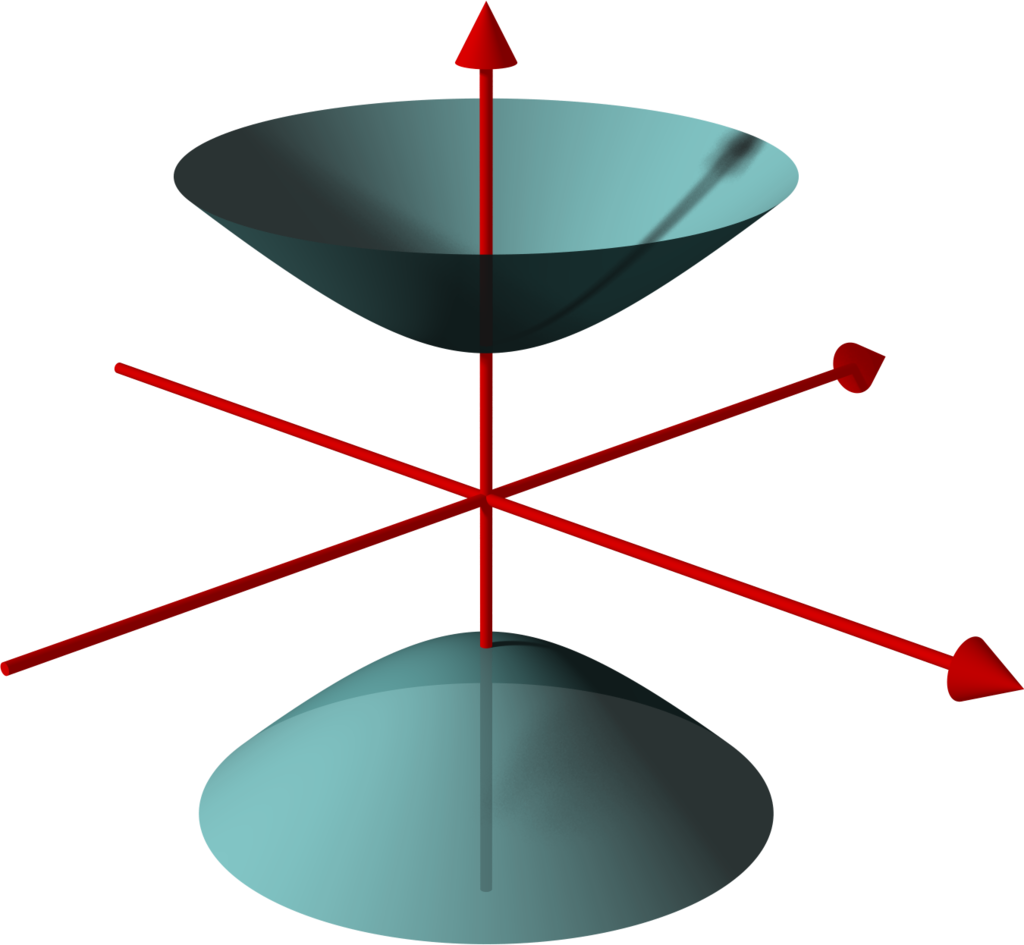
Is that not a sphere cut in half and turned inside out? Instead of cutting a sphere then turning the two halves against each other, why not leave them together and turn our perceptions inside-out? Seems simpler to me, except... well, who knows how to turn their perceptions inside out? And so this approach never occurs to others.

This is EXACTLY the kind of weird, counter-intuitive inversion that I'm used to seeing in other concepts that originate within the realm of excluded middle logic. In fact, it's now the best illustration of this problem I've yet encountered. (I do get that most people won't see what I'm seeing yet, because I'm basically pointing directly at the excluded middle which everyone has learned to exclude and therefore, for people as slow as me, it takes years to learn how to see.) The plot thickens even further when you see what's happening behind the scenes with the Poincare disk:

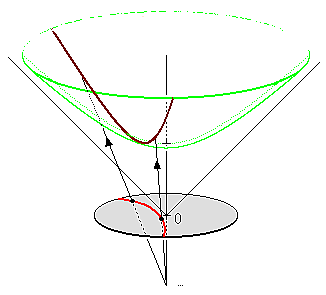
That's a hyperbolic surface being projected onto a Poincare disk in order that you can get a visual on how a curved line (in red) on the flat disk is the shadow of a hyperbolic line embedded within a shape which is itself extremely similar to the inside of a sphere (one-half of it). So similar I now wonder what the real difference is, beyond the endlessness implied by the outer edge of the hyperbola (which could easily be mapped to the fact that when you're inside a sphere you see no edge to the surface, in the way that you can see an edge from the outside of a sphere).**

So, going back to the two-sheet hyperbola example, do we know why we're using two outward-facing hyperbolic curves instead of simply the two insides of sphere, since they are obviously so similar in this illustration? It's one of those things that nobody sees. I think that's the last piece I need to track down. Well, that, and why Gaussian curvature may not be a fine enough measure for the true nature of Hyperbolic geometry, even though it lines up nicely for Elliptic and Euclidean geometries...

Update, later: In answer to my own musing, I will note that Riemannian geometry handles the problem of infinity rather elegantly by placing it as a single point at the North Pole of a sphere... why can't "hyberbolic" geometry do the same thing from the inside? I think it can (simply shrink the equator example I just mentioned to a point***), and I'm going to start calling this geometry something like innerspheric instead of hyperbolic, although I should probably research that term before I do, just in case the New Age-types have trademarked it. The hyperbola was originally derived from conic geometry, but can also be done using spheres.

In conclusion, I really thought I might eventually find good reason to reject my naive hunch -- that happens a lot -- but instead I'm finding more confirmation the deeper I get. I'm now fairly certain I've stumbled upon the best way to illustrate the class of weird-inversion problems we get by over-relying on excluded-middle logic. This is marvellous. Or, as Gauss would put it, "remarkable."

* On a related note, the Poincare disc which is said to contain the entire hyperbolic universe, is a flat circle. Being a circle, it is much more intuitively elegant than the weird open-ended saddle surface of the earlier illustration. In other words, rotating this illustration to include it within ASCII, ")(" is not as elegant as "O" or, even more simple: ")(" is less elegant than "()". This is because the former presents a much more complex surface -- and discontinuities -- than the smooth O-shape.

** In the context of a sphere, it would be like saying the equator represents infinity, which is not exactly intuitive... at least, using outside-in logic. Inside-out logic... doesn't do division. It's that part of mathematics which is indivisible by all the divisioning which happens throughout mathematics. It's the math that operates on the inside of a sphere, where converging and diverging infinities meet somehow, and become one.

*** Yes, this is an update to an update in an article that stumbles and lurches to the point it's making, but it's now nearly two years since I wrote this post, and I have learned more: I can now see that the "point" is not on the surface of the sphere like it is for Riemann, nor along the equator like it is for Poincare, but is at the center of the sphere, with a path leading to it from the "north pole" point of Riemann (the path goes all the way through the center to the south pole, which ultimately converts the sphere into a kind of torus, but that's a whole 'nother conversation). Thus, the hyperbolic disk invented by Poincare is a step in the right direction, but it needs to be inverted, with infinity mapped to the center, not the edge...