I'm coming at this from a number of angles; not all of them are making an appearance in this series of posts. Here's one, though: I got a few more insights in conversation yesterday with a friend who said "What? You don't know calculus? I thought by all your math posts online you knew basics like calculus."
"No, I understand math intuitively, not logically..." I responded, attempting an explanation about how I approach math. He kindly responded by launching into a basic explanation of calculus without realizing what I was saying.
After a couple minutes of trying to figure out what he was saying, I interrupted: "No, thanks, I won't learn calculus that way. I don't think like that. I need pictures." I described better how intuition works. He paused for a minute, then quickly changed from talking about abstract slopes and curves to walking up and down rolling hills in a landscape somewhere. I imagined Ireland. 
Okay so finally I had an image in my mind and I could follow the conversation better.
(Was it that easy all along? You might say "Why didn't you figure that out yourself, you could have imagined rolling hills back when he was talking about slopes and curves all by yourself, or heavens, why not when your math teacher was talking about calculus clear back in high school!" and that's because you don't think like me: that step is not so easy for everyone. I guess I need someone to show me each little tiny step of the way, or I can't see the next step. Once I see it, I get it forever, but until I see it, I'm blind as a statue. It's not that I'm stupid so much as that I'm presented with too much information in the incremental "unknown" moment: To me, that "next step" of imagining myself on the rolling hills of Ireland when someone starts talking about calculus slopes and curves is not an obvious thought -- I have no way to know if the rolling hills of Ireland are relevant to the slopes and curves of calculus until someone says so, probably has something to do with being punished for daydreaming so often as a child, and thus learning to keep my rolling hills separate from my slopes and curves. Don't get me wrong, I can triangulate from two premises to a third and then a conclusion, but I can't always attach the correct visualization to a given abstraction... or at least that's how I organize this limitation in my mind at present. Maybe that's what stupid is, though. Maybe I really am stupid, in spite of my protestations that I'm not...).
Anyway somewhere in the conversation, a little bit after he equated a tangent with a derivative -- which was helpful because I already knew the tangent was a line that barely touches a curve* -- he pointed out how "the derivative is the slope of the curve right at the point where you're standing on the rolling hill."
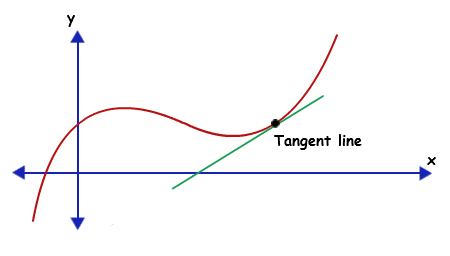Suddenly I realized that a hill could have thousands of derivatives. All the way up till then I've been reading about derivatives, imagining the derivative as something that somehow summarized the whole sine wave, the whole curve, not just a tiny portion of it. As soon as it was clear that a rolling hill has many derivatives, a bunch of stuff I had been reading fell into place at once. "Thanks," I said when he concluded, sincerely grateful for the micro-tutorial. He went on a little further by talking about Fourier transforms and sine waves, some of which I already understood and some of which I didn't listen to because I was already thinking about derivatives.
Onward and upward. I continued today, searching for "derivative intuition" and came upon the video at the bottom of this post (after wading through another heap of non-intuitive websites that thought they were intuitive). Given the insight from my friend above, I was finally able to make it all the way through this video, and now I'm starting to understand the previously-incoherent math formula at the heart of calculus, including that funky E sigma squiggle, which I've seen so many times but always ignored because, well, because I never needed it.
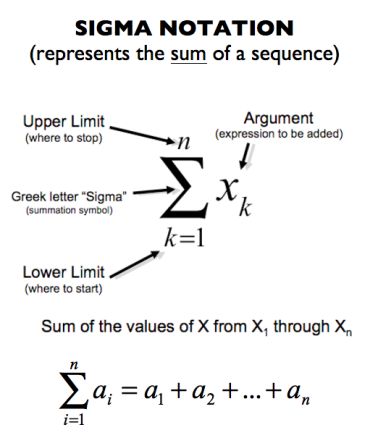Although this video has lame audio quality, it succinctly (ten minutes) covers the reasoning behind creating all these temporary rectangles in order to figure out the area beneath a curve. I guess I'll figure out later why the area beneath a curve is useful. The video ends by indicating I need to learn about anti-derivatives, so off I go learning what that means.
Now that I have a sense for what derivatives are, I think I'm close to going back to learning about neural nets, but I also think I'm almost ready to write another post on some deeper reasons why I avoided calculus all my life, including why I think it's a bit of prestidigitation to cover over a deep crack somewhere near the foundations of math.
https://www.youtube.com/watch?v=LkdodHMcBuc
Footnote
* okay, so you followed the asterisk all the way down here. After years of pondering since high school math, I still can't figure out how a tangent line can touch a single "point" of a curve. Doesn't make sense, seems like the only way to touch a single point of a curve with a straight line is to arrive at a right angle to the curve; otherwise, you kinda bump into two or three points minimum. This concern is related to the prestidigitation mentioned in the last sentence above. Carry on.