Clearhat

A few months ago, I found that one of the more beautiful ideas I had been developing alone for several years had already been discovered by other mathematicians, who had published rigorous papers on the idea. While my own insights were not yet rigorous, they were developed well enough that I quickly recognized them in the work of others, and could also see areas which they had not yet seen. Far from being disappointed that others had discovered these ideas "before me", I was elated. I wrote a weblog post at the time, delighting in the moment that I realized one of my "crackpot" ideas was actually quite solid after all.

Well it happened again. And this time, although I'm elated again, I also write with some caution because the overlap between my insights and the rich detail presented in a video posted by Norman Wildberger (uploaded a few years ago) is so obvious that some might think my ideas are derivative of his. However, they are not. I'm writing this now to document the moment I become aware of this overlap, partly so that in the future, no one thinks my insights are "merely" derivative. I will, in fact, adopt some of his ideas, because they are overall very well thought-out, but I can already see that some of the things I'll be writing about in the future have not yet been covered by Wildberger.

Wildberger is a teacher who famously explores not only conventional mathematics, but he often goes beyond in interesting ways. Within the mathematics community, he's known for his work to resurrect an intuitionist perspective which was more popular a century ago. He feels that the development of infinity and real numbers went in the wrong direction at that time. As a fellow intuitionist, I fully agree, but I also recognize it's a minority position within the math world. Many mathematicians think his ideas in this area are a waste of time.

Nevertheless, Wildberger has hundreds of videos teaching conventional math concepts, sometimes at quite advanced levels far beyond my ability to follow. I'm impressed by what he's done in developing "rational trigonometry," which is a way of doing trigonometry that is easier to understand, being more intuitive. Again, some people dismiss these ideas as irrelevant, but a recent paper showed how his ideas are more efficient for calculating rotations¹. Any videogame developer, who uses such math extensively, will recognize this is a remarkable claim well worth investigating. Although this is outside of my scope of study, it's clear he clearly plays with concepts in a (concrete, sensible, intuitive) way that is similar to how I've been playing with concepts. It's natural that there would be some overlap. What surprises me is how few others have explored these areas.

Computable math is the math of the future

I believe Wildberger's efforts will be better respected in the future than the present. For example, I am confident that, as Artificial Intelligence gains true sentience and begins evaluating mathematics in a more objective way than humans do, the emerging cyberintelligence will incline toward Wildberger's style of mathematics.

I say this partly because his flavor of mathematics is literally called "computable" because of its finite, concrete nature. But I also say this because the Cyber Intelligence will eventually become smart enough to unravel nonsense like the Banach-Tarski paradox. This paradox is a huge problem with consequences which are simply ignored by most mathematicians because they do not realize how the Axiom of Choice reveals a flaw in the axiom of infinity and enables logical paradoxes out of thin air -- but I digress, so let me return to the point:

As a teacher, Wildberger carefully goes in small steps from one concept to the next, where others often skip large sections. This approach is useful for intuitives like me, so I've visited his videos on various topics over the years.

Looking into the history of zero and the advent of negative numbers

Today's experience is remarkable and unique, so I want to talk about it a little. I spent the past several days contemplating a subject that I've studied off and on for years, always without diving deep because I was pursuing other things, and this was often a side note to those other pursuits. Finally, this weekend, I decided to start fleshing out the details of an intuitive hunch that there was a "mistake" made in the history of mathematics that had to do with the introduction of zero and the related development of negative numbers.

I began thinking about what mathematics would look like if that mistake were rigorously identified and fixed; how different would it be? So in every idle moment over the past few days, I contemplated the "correct" way to work with zero and negative numbers, and made several small breakthroughs.

Finally, I made a bigger breakthrough, which was to know with certainty that I needed to be able to clearly distinguish negative numbers from the operation of subtraction. I'd encountered this insight before, but now I had the confirmation needed to nail it down. As it turns out, these are two completely different things: The notation of negative numbers -- which is the same notation for a minus sign -- needs to be better defined. But which one should change, the minus or the negative? And how?

As I was doing a lot of driving, I had no notepad, so I resolved to develop the notation at some point in the near future. With that decided, I began doing some basic operations in my head, testing out the new theory, seeking to derive some basic rules to define the new approach. Without notation, I was keeping track of what happens in my mind, as I added, subtracted, multiplied, and divided positives and negatives with this new symmetry. It turns out, in most instances, the math lines up the same as what we're all used to, but in a few spots, the answers are quite different.

My goal in workng on negative numbers this way is to lay a foundation that can be used later, when complex numbers are introduced upon this foundation, which resolves the awkwardness of noncommutative operations². On one level, I'm trying to develop the methods and notation to allow quaternions -- or something like them -- to be commutative. I've often wondered if the awkwardness with noncommutativity is rooted, not in the way complex numbers work, but further back in history, maybe with an innovation like negative numbers. It seems obvious to me: they should operate symmetrically with positive numbers. Specifically, when multiplying negative numbers, the result should be a mirror of what happens when multiplying positive numbers. But instead, if you multiply two negative numbers, we have all been taught the answer must be positive. This is not a mirror of what happens when you multiply two positive numbers. It's an anomaly.

Why I believe we are not symmetrical with multiplying negatives

I think I know why this happens on an intuitive level, because one of the most interesting thought experiments in my life was on this point, a few months ago. I'll briefly describe what happened:

I tried to place my mind something like 1500 years into the past, into the minds of those who were inventing zero and negative numbers, not just in India and Arabia, but in European minds as the ideas slowly spread. Why did they make the decisions they made? What were they thinking about? Surely, they were trying various ways of doing this. So I was experimenting with what it "feels" like to multiply two negative numbers and move toward a further negative destination (rather than what we do now, which is to reverse direction and head back to the positive side).

As I did this, with eyes closed so I could concentrate better, I suddenly felt the focus of my mathematical mind moving toward a darkness, an endless abyss, into which I might fall, forever. I reacted with fear, retreating back toward the safety of positive numbers. This was a completely unanticipated sensation, which the rational mathematication would never experience, but which an intuitive mathematician might recognize. (The intuitive mathematician navigates with pictures and images and structures and feelings. The rational mathematician navigates with abstractions and symbols. Poincaré wrote about these two different kinds of mathematicians a hundred years ago, and others have, too, so I won't go into it here.)

I knew then, that the long-ago mathematicians, with a historically more implicit fear of the void (they literally called it horror vacui, a term we've nearly forgotten), were reacting to a similar sensation within their minds, when they decided that multiplying two negatives should equal a positive.

Perhaps the sensation was subliminal to them, but -- for one brief instant -- it was very real for me, and maybe it was for some of them. I cannot easily forget that moment. Every now and then I remember and contemplate how curious it was to feel a sensation of fear from simply multiplying two negative numbers while contemplating what would result if the answer were further negative.

Let me be very clear about this point, because it is so out-of-the-box. First, let me set some background:

Suppose that "infinity," a boundless greatness, can be compared to God, and heaven -- not such a difficult thing to imagine for people 1500 years ago or more. Is "the greatest number" something like "the greatest being," God? Can you imagine what it would be like, inventing the idea of negative infinity, and then being scared of what you've invented because it overlapped the same psychological space in your mind as the logical opposite of God and heaven, meaning hell, and the devil?

If you think this example is overwrought, it may help you to know that there was great resistance to the idea of zero, much less negative numbers, for centuries. Why? Ancient Greeks resisted the philosophical idea of "the void" specifically because it was associated with the devil. If you laugh at this idea, you're not getting the point.

I believe I was able to experience this abyss the way I did partly because I had, much earlier, developed a reliable way to unite positive infinity and negative infinity into a single thing. To me, negative infinity is not something that represents the opposite of positive infinity -- it is identical, the same thing. There is only a single infinity. (In fact, this is a central part of the "beautiful ideas" I mentioned earlier, which align with Wheel Theory.)

So when I experienced that abyss briefly, it was: 1.) while standing on solid philosophical ground, knowing that the abyss was merely a perceptual glitch in my internal math world, not a real thing, and 2.) while intentionally trying to place myself in the shoes of someone many centuries earlier. Thus, I was insulated: my subconscious was able to bring the experience into conscious awareness in a way that was scary, but less disturbing to me than it would be for them. Even still, I felt the fear, and retreated back to safety.

Think about this for a second. This was a conscious experience for me, but it might remain unconscious to others. All they would know consciously is that it "makes sense" for two negatives to multiply into a positive, whereas it just "feels wrong" to let two negatives multiply more deeply toward negative infinity.

So although it's kind of "out there," it can be defended within reason, and I believe that's the historical, intuitive reason why multiplying two negatives produces a positive, in all math textbooks available today.

There is also a technical reason, which is the one I was resolving over this weekend: When you make two negatives multiply toward a more negative answer, you then need a way to keep track of what's happening a little more carefully than we're used to. This is because you can no longer use the same sign to mean "negative" and "minus." These mean two different things, a fact which is hidden by the way we currently do math. If the people who invented negative numbers would have revealed this hidden fact (perhaps some tried?), it would have changed the way we think about positive numbers. (It would have been a good change, though, as it is very likely that complex numbers would have been invented much sooner if this had happened. And more: The way we understand zero would have been quite different. Insights like Wheel Theory would have also developed much sooner. They would not be obscure and on the periphery of mathematics, but closer to the center).

The gravitational pull of zero

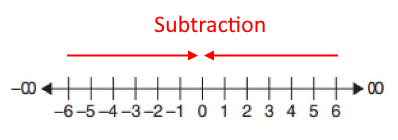What I determined, in my thought experiments over the weekend, was that when it comes to subtraction, "zero" has a kind of gravitational pull to it. Not scary like the devil's abyss that I described earlier, but in a neutral way, like a magnet.

When you subtract a number, you first define a starting point and then your result will end up being somewhere "toward the zero." When you add a number, your result appears "further away from the zero."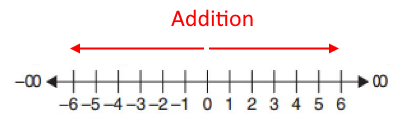

This "direction" defines the first step of the new subtraction operation. The second step is determined by the sign of the number being subtracted. If it is positive, follow the initial direction (inward); if it is negative, reverse direction and go outward.

Note both of these steps already describe what happens with the right side of the number line. It's a novel idea to symmetrically do this on the left side. Thus the direction of subtraction is not always "leftward" as we've all been taught: it is oriented around the zero, and operates "inward" toward the zero. Although negative numbers always count "leftward," subtraction can go either way, depending on context.

Here are some of the thought experiments I was doing:

• Five plus negative five is zero.
• Five minus negative five is ten.
• Five times positive five is twenty-five.
• Negative five times negative five is negative twenty-five, not twenty-five.
• Negative twenty-five divided by five is negative five.
• Negative twenty-five divided by negative five is negative five, not five³.

This is the basic idea of what I had worked out over the weekend. The key insight was that everything is oriented around zero, that "subtraction moves inward." I'm pleased that I figured that out independently, because I later realized this aligns very well with ideas I've already worked out which are similar to Wheel Theory. This is a nice confirmation that I'm moving in coherent direction.

And then today, I randomly⁴ stumbled into Wildberger's video on what he calls the "true" complex numbers. The moment I saw his notation of the "bar" over the negative numbers, I knew he had encountered the same puzzle I just described above, and solved it with the notation which distinguishes negative numbers from subtraction.

As I continue watching, I see he has rigorously worked out many more details, much more than me in some areas, but there are a few key places where he hasn't figured out what's going on underneath it all. He would figure things out pretty quickly if he studied Wheel Theory, but for now, I'll keep quiet and leave things where they are, because I hope to be able to publish some things myself someday.

For now, I'm delighted that this experience has now happened twice: Working for years alone on a subject, thinking that it was nonsensible to others, and then discovering that "real" mathematicians recently developed the same subject, and laid a foundation making it easier for an amateur like me to take the next steps.

Footnotes

1. The paper concludes: "The proposed method is faster, easy to program and requires less memory."
2. Just discovered the "awkwardness" of noncommutative operations is actually an artifact of physics, not of math -- it's the way physics works, so it will never be "resolved" as I was intending. However, it's been while pursuing a noncommutative way of describing rotations that I discovered many wonderful things, so even though I just now learned I was wrong on this point, I have no regrets. I'm glad I figured this out _before_ I publish anything. (I mean, publish in a journal, not a weblog.)
3. While writing this, it's occurred to me that this conventional rule: "When multiplying a positive and a negative, the product will always be negative. It doesn't matter what order the signs are in" is... asymmetrical. And in keeping with my insight about defining the "starting point," this is where noncommutativity fits into the conventional number line. People think this came into being with complex numbers a couple centuries ago, but really, this goes all the way back in history to the innovation of negative numbers at least 15 centuries ago. Here is a key to how it works: If you multiply negative five times five, you will get a different answer than if you multiply five times negative five. The answer depends on whether you're starting on the right or the left side of the zero. Here's the most interesting part: if we had been smart enough to invent negative numbers with the approach I'm describing now, we would most certainly have figured out the mathematics of 3-D rotations long before Hamilton's quaternions, because we'd already be familiar with noncommutativity. Someone like Newton, Leibniz, Euler or even earlier would have seen how this was essential for rotations (which is what drove Hamilton's discovery). The implications here are staggering. Why has no one seen this before now?
4. "Randomly" means YouTube presented a link to Wildberger in their front page montage, which I was randomly skimming during an idle moment, with no idea I was about to stumble into this exact subject that I'd been contemplating all weekend. I'm being clear about this because this kind of non-random "random" event has happened many times throughout my study of these ideas.